Chapter 1: Real Numbers

Euclid’s Division Lemma:

Given positive integers a and b, there exists unique integers q and r satisfying a = bq + r, where 0 ≤ r < b

• Lemma is a proven statement used for proving another statement.

Euclid’s Division Lemma states that given two integers a and b, there exists a unique pair of integers q and r such that a = b × q + r and 0 ≤ r < b.

This lemma is essentially equivalent to: dividend = divisor × quotient + remainder

In other words, for a given pair of dividend and divisor, the quotient and remainder obtained are going to be unique.

Euclid’s Division Algorithm:

• An algorithm is a series of well defined steps which gives a procedure for solving a type of problem.
• This algorithm is a technique to compute the H.C.F of two given positive integers.
• According to this algorithm, the HCF of any two positive integers ‘a’ and ‘b’, with a > b, is obtained by following the steps given below:

Step 1: Apply Euclid’s division lemma, to ‘a’ and ‘b’, to find q and r, such that a = bq + r, 0 ≤ r < b.

Step 2: If r = 0, the HCF is b. If r ≠ 0, apply Euclid’s division lemma to b and r.

Step 3: Continue the process till the remainder is zero. The divisor at this stage will be HCF (a, b). Also, note that HCF (a, b) = HCF (b, r).

Euclid’s Division Algorithm can be summarized as follows:

• Euclid’s Division Algorithm is stated for only positive integers but it can be extended for all integers except zero, i.e., b ≠ 0.

Consider two numbers 78 and 980 and we need to find the HCF of these numbers. To do this, we choose the largest integer first, i.e. 980 and then according to Euclid Division Lemma, a = bq + r where 0 ≤ r < b;

980 = 78 × 12 + 44

Now, here a = 980, b = 78, q = 12 and r = 44.

Now consider the divisor 78 and the remainder 44, apply Euclid division lemma again.

78 = 44 × 1 + 34

Similarly, consider the divisor 44 and the remainder 34, apply Euclid division lemma to 44 and 34.

44 = 34 × 1 + 10

Following the same procedure again,

34 = 10 × 3 + 4

10 = 4 × 2 + 2

4 = 2 × 2 + 0

As we see that the remainder has become zero, therefore, proceeding further is not possible. Hence, the HCF is the divisor b left in the last step. We can conclude that the HCF of 980 and 78 is 2.

Let us try another example to find the HCF of two numbers 250 and 75. Here, the larger the integer is 250, therefore, by applying Euclid Division Lemma a = bq + r where 0 ≤ r < b, we have

a = 250 and b = 75

⇒ 250 = 75 × 3 + 25

By applying the Euclid’s Division Algorithm to 75 and 25, we have:

75 = 25 × 3 + 0

As the remainder becomes zero, we cannot proceed further. According to the algorithm, in this case, the divisor is 25. Hence, the HCF of 250 and 75 is 25.

Real Numbers:

• The numbers which can be represented in the form  of where p and q are integers and q ≠ 0 are called Rational numbers.
• Any number that cannot be expressed in the , form of , where p and q are integers and q ≠ 0 are called Irrational numbers.
• There are more irrational numbers than rational numbers between two consecutive numbers.
• Rational and Irrational numbers together constitute Real numbers.

Properties of Irrational numbers:

1. The Sum, Difference, Product and Division of two irrational numbers need not always be an irrational number.
2. Negative of an irrational number is an irrational number.
3. Sum of a rational and an irrational number is irrational.
4. Product and Division of a non-zero rational and irrational number is always irrational.

Fractions:

• Terminating fractions are the fractions which leaves remainder 0 on normal division.
• Recurring fractions are the fractions which never leave a remainder 0 on normal division.

Properties related to prime numbers:

• If p is a prime and divides a², then p divides a, where ‘a’ is a positive integer.
• If p is a prime, then  is an irrational number.
• A number ends with the digit zero if and only if it has 2 and 5 as two of its prime factors.
• Decimal Expansion:
• The decimal expansion of rational number is either terminating or non-terminating recurring (repeating).
• If the decimal expansion of rational number terminates, then we can express the number in the form of , where p and q are co-prime, and the prime factorization of q is of the form 2ⁿ5^m, where n and m are non negative integers.
• If  is a rational number, such that the prime factorization of q is of the form 2ⁿ5^m, where n, m are non-negative integers. Then, x has a decimal expansion which terminates.
• If the denominator of a rational number is of the form 2ⁿ5^m, then it will terminate after n places if n > m or after m places if m > n.
• The decimal expansion of an irrational number is non-terminating, non-recurring.

Fundamental Theorem of Arithmetic:

Every composite number can be expressed (factorized) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.

The procedure of finding HCF (Highest Common Factor) and LCM (Lowest Common Multiple) of given two positive integers a and b:

1. Find the prime factorization of given numbers.
2. HCF (a, b) = Product of the smallest power of each common prime factors in the numbers.
3. LCM (a, b) = Product of the greatest power of each prime factors, involved in the numbers.

Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers which are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:

35 = 7 × 5

Here, 7 and 5 are the prime factors of 35

Similarly, another number 114560 can be represented as the product of its prime factors by using prime factorization method,

114560 = 27 × 5 × 179

So, we have factorized 114560 as the product of the power of its primes.

Therefore, every natural number can be expressed in the form of the product of the power of its primes. This statement is known as the Fundamental Theorem of Arithmetic, unique factorization theorem or the unique-prime-factorization theorem.

Proof for Fundamental Theorem of Arithmetic: In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.

From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration order of occurrence of the prime factors.

In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:

The prime factorization of any natural number is said to be unique for except the order of their factors.

In general, a composite number “a” can be expressed as,

a = p₁ p₂ p₃ ………… p_n, where p₁, p₂, p₃ ………… p_n are the prime factors of a written in ascending order i.e. p₁ ≤ p₂ ≤ p₃ ………… ≤p_n.

Writing the primes in ascending order makes the factorization unique in nature.

Relationship between HCF and LCM of two numbers:

If a and b are two positive integers, then HCF (a, b) × LCM (a, b) = a × b

Relationship between HCF and LCM of three numbers:

Method of Finding LCM

In Mathematics, the LCM of any two is the value that is evenly divisible by the two givennumbers. The full form of LCM is Least Common Multiple. It is also called the Least Common Divisor (LCD). For example, LCM (4, 5) = 20. Here, the LCM 20 is divisible by both 4 and 5 such that 4 and 5 are called the divisors of 20.

LCM is also used to add or subtract any two fractions when the denominators of the fractions are different. While performing any arithmetic operations such as addition, subtraction with fractions, LCM is used to make the denominators common. This process makes the simplification process easier.

Least Common Multiple (LCM) is a method to find the smallest common multiple between any two or more numbers. A common multiple is a number which is a multiple of two or more numbers.

Properties of LCM

Properties	Description
Associative property	LCM (a, b) = LCM (b, a)
Commutative property	LCM (a, b, c) = LCM (LCM(a, b), c) = LCM(a, LCM(b, c))
Distributive property	LCM (da, db, dc) = d LCM (a, b, c)

LCM Formula

Let a and b are two given integers. The formula to find the LCM of a & b is given by:

LCM (a, b) = (a x b)/GCD (a, b)

Where GCD (a, b) means Greatest Common Divisor or Highest Common Factor of a & b.

LCM Formula for Fractions

The formula to find the LCM of fractions is given by:

L.C.M. = L.C.M Of Numerator/H.C.F Of Denominator

Different Methods of LCM

There are three important methods by which we can find the LCM of two or more numbers. They are:

Listing the Multiples

Prime Factorization Method

Division Method

Listing the Multiples: The method to find the least common multiple of any given numbers is first to list down the multiples of specific numbers and then find the first common multiple between them.

Suppose there are two numbers 11 and 33. Then by listing the multiples of 11 and 33, we get;

Multiples of 11 = 11, 22, 33, 44, 55, ….

Multiples of 33 = 33, 66, 99, ….

We can see, the first common multiple or the least common multiple of both the numbers is 33. Hence, the LCM (11, 33) = 33.

LCM By Prime Factorization: Another method to find the LCM of the given numbers is prime factorization. Suppose there are three numbers 12, 16 and 24. Let us write the prime factors of all three numbers individually.

12 = 2 x 2 x 3

16 = 2 x 2 x 2 x 2

24 = 2 x 2 x 2 x 3

Now writing the prime factors of all the three numbers together, we get;

12 x 16 x 24 = 2 x 2 x 3 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3

Now pairing the common prime factors we get the LCM. Hence, there are four 2’s and one 3. So the LCM of 12, 16 and 24 will be;

LCM (12, 16, 24) = 2 x 2 x 2 x 2 x 3 = 48

LCM By Division Method

• Finding LCM of two numbers by division method is an easy method. Below are the steps to find the LCM by division method:
• First, write the numbers, separated by commas
• Now divide the numbers, by the smallest prime number.
• If any number is not divisible, then write down that number and proceed further
• Keep on dividing the row of numbers by prime numbers, unless we get the results as 1 in the complete row
• Now LCM of the numbers will be equal to the product of all the prime numbers we obtained in the division method

Example: To find the Least Common Multiple (L.C.M) of 36 and 56,

36 = 2 × 2 × 3 × 3

56 = 2 × 2 × 2 × 7

The common prime factors are 2 × 2

The uncommon prime factors are 3 × 3 for 36 and 2 × 7 for 56.

LCM of 36 and 56 = 2 × 2 × 3 × 3 × 2 × 7 which is 504

Method of Finding HCF

H.C.F can be found using two methods – Prime factorisation and Euclid’s division algorithm.

Prime Factorisation: Given two numbers, we express both of them as products of their respective prime factors. Then, we select the prime factors that are common to both the numbers

Example – To find the H.C.F of 20 and 24

20 = 2 × 2 × 5 and 24 = 2 × 2 × 2 × 3

The factor common to 20 and 24 is 2 × 2, which is 4, which in turn is the H.C.F of 20 and 24.

Euclid’s Division Algorithm: It is the repeated use of Euclid’s division lemma to find the H.C.F of two numbers.

Example: To find the HCF of 18 and 30

HCF by Shortcut method

Steps to find the HCF of any given numbers.

Step 1: Divide larger number by smaller number first, such as;

Larger Number/Smaller Number

Step 2: Divide the divisor of step 1 by the remainder left.

Divisor of step 1/Remainder

Step 3: Again divide the divisor of step 2 by the remainder.

Divisor of step 2/Remainder

Step 4: Repeat the process until the remainder is zero.

Step 5: The divisor of the last step is the HCF.

Important Questions

Multiple Choice questions-

1. HCF of 8, 9, 25 is

(a) 8 (b) 9 (c) 25 (d) 1

2. Which of the following is not irrational?

(a)

(b)

(c)

(d)

 3. The product of a rational and irrational number is

(a) rational

(b) irrational

(c) both of above

(d) none of above

4. The sum of a rational and irrational number is

(a) rational

(b) irrational

(c) both of above

(d) none of above

5. The product of two different irrational numbers is always

(a) rational

(b) irrational

(c) both of above

(d) none of above

6. The sum of two irrational numbers is always

(a) irrational

(b) rational

(c) rational or irrational

(d) one

7. If b = 3, then any integer can be expressed as a =

(a) 3q, 3q+ 1, 3q + 2

(b) 3q

(c) none of the above

(d) 3q+ 1

8. The product of three consecutive positive integers is divisible by

(a) 4

(b) 6

(c) no common factor

(d) only 1

9. The set A = {0,1, 2, 3, 4, …} represents the set of

(a) whole numbers

(b) integers

(c) natural numbers

(d) even numbers

10. Which number is divisible by 11?

(a) 1516

(b) 1452

(c) 1011

(d) 1121

       Very Short Questions:

1. What is the HCF of the smallest composite number and the smallest prime number?
2. The decimal representation of  will terminate after how many places of decimal?
3. If HCF of a and b is 12 and product of these numbers is 1800. Then what is LCM of these numbers?
4. What is the HCF of 3³ × 5 and 3² × 5²?
5. if a is an odd number, b is not divisible by 3 and LCM of a and b is P, what is the LCM of 3a and 2b?
6. If P is prime number then, what is the LCM of P, P², P³?
7. Two positive integers p and q can be expressed as p = ab² and q = a²b, a and b are prime numbers. What is the LCM of p and q?
8. A number N when divided by 14 gives the remainder 5. What is the remainder when the same number is divided by 7?
9. Examine whether  is a terminating decimal or not.
10. What are the possible values of remainder r, when a positive integer a is divided by 3?
11. A rational number in its decimal expansion is 1.7351. What can you say about the prime factors of q when this number is expressed in the form  ? Give reason.
12. Without actually performing the long division, find  will have terminating or non. terminating repeating decimal expansion. Give reason for your answer.

Short Questions :

1. Can the number 4ⁿ, n be a natural number, end with the digit 0? Give reason.
2. Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer.
3. Can two numbers have 18 as their HCF and 380 as their LCM? Give reason.
4. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
5. Find the LCM and HCF of 12, 15 and 21 by applying the prime factorisation method.
6. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.

(1) 26 and 91 (ii) 198 and 144

• There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start from the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
• Write down the decimal expansiwns of the following numbers:

(i)  (ii)

• Express the number  in the form of rational number .
• If n is an odd positive integer, show that (n² – 1) is divisible by 8.
• The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.
• Find the value of x, y and z in the given factor tree. Can the value of ‘x’ be found without finding the value of ‘y’ and ‘z’? If yes, explain.

1. Show that any positive odd integer is of the form 6q + 1 or 6q + S or 6q + 5 where q is some integer.
2. The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form . What can you say about the prime factors of q?

(i) 0.140140014000140000… (ii)

Long Questions :

1. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
2. Show that one and only one out of n, n + 2, n + 4 is divisible by 3, where n is any positive integer.
3. Use Euclid’s division algorithm to find the HCF of:

(i) 960 and 432

(ii) 4052 and 12576.

• Using prime factorisation method, find the HCF and LCM of 30, 72 and 432. Also show that HCF × LCM ≠ Product of the three numbers.
• Prove that √7 is an irrational number.
• Show that 5 – √3 is an irrational number.
• Using Euclid’s division algorithm, find whether the pair of numbers 847,2160 are co-prime or not.
• Check whether 6ⁿ can end with the digit O for any natural number n.
• Show that there is iw positive integer n for which  is rational.
• Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.

Case Study Questions:

1. Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. Answer them.
2. For what value of n, 4n ends in 0?
3. 10
4. When n is even.
5. When n is odd.
6. No value of n.
7. If a is a positive rational number and n is a positive integer greater than I, then for what value of n, 4n is a rational number?
8. When n is any even integer.
9. When n is any odd integer.
10. For all n > 1.
11. Only when n = 0.
12. If x and y are two odd positive integers, then which of the following is true?
13. x² + y² is even.
14. x² + y² is not divisible by 4.
15. x² + y² is odd.
16. Both (a) and (b).
17. The statement ‘One of every three consecutive positive integers is divisible by 3’ is:
18. Always true.
19. Always false.
20. Sometimes true.
21. None of these.
22. If n is any odd integer, then n2 – 1 is divisible by:
23. 22
24. 55
25. 88
26. 8
27. Real numbers are extremely useful in everyday life. That is probably one of the main reasons we all learn how to count and add and subtract from a very young age. Real numbers help us to count and to measure out quantities of different items in various fields like retail, buying, catering, publishing etc. Every normal person uses real numbers in his daily life. After knowing the importance of real numbers, try and improve your knowledge about them by answering the following questions on real life based situations.
28. Three people go for a morning walk together from the same place. Their steps measure 80cm, 85cm and 90cm respectively. What is the minimum distance travelled when they meet at first time after starting the walk assuming that their walking speed is same?
29. 6120cm
30. 12240cm
31. 4080cm
32. None of these
33. ln a school Independence Day parade, a group of 594 students need to march behind a band of 189 members. The two groups have to march in the same number of columns. What is the maximum number of columns in which they can march?
34. 9
35. 6
36. 27
37. 29
38. Two tankers contain 768 litres and 420 litres of fuel respectively. Find the maximum capacity of the container which can measure the fuel of either tanker exactly.
39. 4 litres
40. 7 litres
41. 12 litres
42. 18 litres
43. The dimensions of a room are 8m, 25cm, 6m, 75cm and 4m, 50cm. Find the length of the largest measuring rod which can measure the dimensions of room exactly.
44. 1m, 25cm
45. 75cm
46. 90cm
47. 1m, 35cm
48. Pens are sold in pack of 8 and notepads are sold in pack of 12. Find the least number of pack of each type that one should buy so that there are equal number of pens and notepads.
49. 3 and 2
50. 2 and 5
51. 3 and 4
52. 4 and 5

Assertion Reason Questions-

1. Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
2. Both A and R are true and R is the correct explanation of A.
3. Both A and R are true and R is not the correct explanation of A.
4. A is true but R is false.
5. A is false but R is true.

Assertion: 11 × 4 × 3 × 2 + 4 is a composite number.

Reason: Every composite number can be expressed as product of primes.

• Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
• Both A and R are true and R is the correct explanation of A.
• Both A and R are true and R is not the correct explanation of A.
• A is true but R is false.
• A is false but R is true.

Assertion: If LCM = 350, product of two numbers is 25 × 70, then their HCF = 5
Reason: LCM × product of numbers = HCF

Answer Key-

Multiple Choice questions-

1. (d) 1
2. (c)
3. (b) irrational
4. (b) irrational
5. (b) irrational
6. (a) irrational
7. (a) 3q, 3q+ 1, 3q + 2
8. (b) 6
9. (a) whole numbers
10. (b) 1452

Very Short Answer :

1. Smallest composite number = 4

Smallest prime number = 2

So, HCF (4, 2) = 2

•  

This representation will terminate after 4 decimal places.

• Product of two numbers = Product of their LCM and HCF

⇒ 1800 = 12 × LCM

⇒ LCM

• HCF of 3³ × 5 and 3² × 5² = 3² × 5 = 45
• 6P
• P³
• a²h²
• 5, because 14 is multiple of 7.

Therefore, remainder in both cases are same.

•  

Since the denominator has 3 as its factor.

  is a non4ermznatlng decimal.

1. According to Euclid’s division lemma

a = 3q + r, where O r < 3 and r is an integer.

Therefore, the values of r can be 0, 1 or 2.

1. As 1.7351 is a terminating decimal number, so q must be of the form 2^m 5ⁿ, where in, n are natural numbers.
2. and 500 = 22 × 53, so it has terminating decimal expansion.

Short Answer :

1. if 4ⁿ ends with 0, then it must have 5 as a factor. But, (4)ⁿ = (2²)ⁿ = 2²ⁿ i.e., the only prime factor.

of 4ⁿ is 2. Also, we know from the fundamental theorem of arithmetic that the prime factorization of each number is unique.

∴ 4ⁿ can never end with 0.

• No, because any positive integer can be written as 3q, 3q + 1, 3q + 2, therefore, square will be

9q² = 3m, 9q² + 6q + 1 = 3(3q²+ 2q) + 1 = 3m + 1,

9q² + 12q + 4 = 3(3q²+ 4q + 1) + 1 = 3m + 1.

• No, because here HCF (18) does not divide LCM (380).
• For the maximum number of columns, we have to find the HCF of 616 and 32.

Now, since 616 > 32, we apply division lemma to 616 and 32.

We have, 616 = 32 × 19 + 8

Here, remainder 8 ≠ O. So, we again apply division lemma to 32 and 8.

We have, 32 = 8 × 4 + O

Here, remainder is zero. So, HCF (616, 32) = 8

Hence, maximum number of columns is 8.

• The prime factors of 12, 15 and 21 are

12 2² × 3, 15 = 3 × 5 and 21 = 3 × 7

Therefore, the HCF of these integers is 3.

2², 3¹, 5¹ and 7¹ and are the greatest powers involved in the prime factors of 12, 15 and 21.

So, LCM (12, 15, 21) = 2² × 3¹ × 5¹ × 7¹ = 420.

• (i) We have, 26 = 2 × 13 and 91 = 7 × 13

Thus, LCM (26, 91) = 2 × 7 × 13 = 182

HCF (26, 91) = 13

Now, LCM (26, 91) × HCF (26, 91) = 182 × 13 = 2366

and Product of the two numbers = 26 × 91 = 2366

Hence, LCM × HCF = Product of two numbers.

(ii) 144 = 24 × 32 and 198 = 2 × 32 × 11

∴ LCM(198,144)24 × 32 × 11 = 1584

HCF(198, 144) = 2 × 32 = 18

Now, LCM (198, 144) × HCF (198, 144) = 1584 × 18 = 28512

and product of 198 and 144 = 28512

Thus, product of LCM (198, 144) and HCF (198, 144)

= Product of 198 and 144.

• To find the time after which they meet again at the starting point, we have to find LCM of 18 and 12 minutes. We have

Therefore, LCM of 18 and 12 = 2² × 3² = 36

So, they will meet again at the starting point after 36 minutes.

• (i)

(ii)

• Let x =

then x = 0.3178178178 … … (i)

10x = 3.178178178 … …(ii)

10000x = 3178.178178… …(iii)

On subtracting (ii) from (iii), we get

1. We know that an odd positive integer n is of the form (4q + 1) or (4 + 3) for some integer q.

Case – I When n = (4q + 1)

In this case n² – 1 = (4q + 1)²1 = 16q² + 8q = 8q(2q + 1)

which is clearly divisible by 8.

Case – II When n = (4q + 3)

In this case, we have

n2² = (4q + 3)² – 1 = 16q² + 24q + 8 = 8(2q²+ 3q + 1)

which is clearly divisible by 8.

Hence (n² – 1) is divisible by 8.

1. Let HCF of the numbers hex then according to question LCM of the number will be 14x

And x + 14 = 600 ⇒ 15x = 600 ⇒ x = 40

Then HCF = 40 and LCM = 14 × 40 = 560

∵ LCM × HCF = Product of the numbers

560 × 40 = 280 × Second number Second number  

Then other number is 80.

1. z = 2 × 17 = 34; y = 34 × 2 = 68 and x = 2 × 68 = 136

Yes, value of x can be found without finding value of y or z as

x = 2 × 2 × 2 × 17 which arc prime 1tctors of x.

1. Let a he any positive odd integer and h = 6. Then, by Euclid’s algorithm, a = 6q + r, for some

integer q ≥ O and O ≤ r < 6.

i.e., the possible remainders are 0, 1, 2, 3, 4, 5.

1’hus,a canbeoftheform6q,or6q + I,or6q + 2,orßq + 3,ör6q + 4,

or 6q + 5, where q is some quotient.

Since a. is odd integer, so a cannot be of the form , or + 2, or 6q + 4, (since they are even).

Thus, a is of the form 6q + 1, 6q + 3, or 6q + 5, where q is some integer.

Hence, any odd positive integer is of the form 6q + 1 or 6q -1- 3 or 6q + 5, where q is sorne integer.

1. (i) We have, 0.140140014000140000… a non-terminating and non-repeating decimal expansion. So it is irrational. It cannot be written in the form of

(ii) We have,  a non-terminating but repeating decimal expansion. So it is rational.

Let x =

Then, x = 0.1616… (i)

100×16.1616… ..(ii)

On subtracting (i) from (ii), we get

100x – x = 16.1616 – 0.1616

⇒ 99x = 16 ⇒ x

The denominator (q) has factors other than 2 or 5.

Long Answer :

1. Let a be an arbitrary positive integer.

Then by Euclid’s division algorithm, corresponding to the positive integers a and 3 there exist

non-negative integers q and r such that

a = 3q + r where 0 ≤ r <3

a² = 9q² + 6qr + r² ….(i) 0 ≤ r <3

Case – I: When r = 0 [putting in (i)]

a² = 9q² = 3(3q²) = 3m where m = 3q²

Case – II: r = 1

a² = 9q² + 6q + 1 = 3(3q² + 2q)+ 1 = 3m + 1 where m = 3q² + 2q

Case – III: r = 2

a² = 9q² + 12 + 4 = 3(3q² + 4q + 1) + 1 = 3m + 1 where m = (3q² + 4q + 1)

Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

• Let q be the quotient and r be the remainder when n is divided by 3.

Therefore, n = 3q + r, where r = 0, 1, 2

n = 3q or n = 3q + 1 or n = 3q + 2

Case (i) if n = 3q, then n is divisible by 3, n + 2 and n +. 4 arc not divisible by 3.

Case (ii) if 71 = 3q + 1 then n + 2 = 3q + 3 = 3(q + 1), which is divisible by 3 and

n + 4 = 3q + 5, which is not divisible by 3.

So, only (n + 2) is divisible by 3.

Case (iii) If n = 3q + 2, then n + 2 = 3q + 4, which is not divisible by 3 and

(n + 4) = 3q + 6 = 3(q + 2), which is divisible by 3.

So, only (n + 4) is divisible by 3.

Hence one and only one out of n, (n + 2), (n + 4), is divisible by 3.

• (j) Since 960 > 432, we apply the division lemma to 960 and 432.

We have, 960 = 432 × 2 + 96

Since the remainder 96 ≠ 0, so we apply the division lemma to 432 and 96.

We have, 432 = 96 × 4 + 48

Again remainder 48 ≠ 0 so we again apply division lemma to 96 and 48.

We have, 96 = 48 × 2 + O

The remainder has now become zero. So our procedure stops.

Since the divisor at this stage is 48.

Hence, HOE of 960 and 432 is 48.

i.e., HCF (960, 432) = 4H

(ii) Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get

12576 = 4052 × 3 + 420

Since the remainder 420 ≠ 0, we apply the division lemma to 4052 and 420, to get

4052 = 420 × 9 + 272

We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get

420 = 272 × 1 + 148

We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get

272 = 148 × 1 + 124

We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get

148 = 124 × 1 + 24

We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get

124 = 24 × 5 + 4

We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get

24 = 4 × 6 + O

The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.

• Given members = 30, 72, 432 .

30 = 2 × 3 × 5; 72 = 23 × 32 and 432 = 24 × 33

Here, 2’ and 31 are the smallest powers of the common factors 2 and 3 respectively.

So, HCF (30, 72, 432) = 21 × 31 = 2× 3 = 6

Again, 2, 33 and 51 arc the greatest powers of the prime factors 2, 3 and 5 respectively.

So, LCM (30, 72, 432) = 24 × 33 × 51 = 2160

HCF × LCM = 6 × 2160 = 12960

Product of numbers = 30 × 72 × 432 = 933120 .

Therefore, HCF × LCM ≠ Product of the numbers.

• Let us assume, to the contrary, that √7 is a rational number.

Then, there exist co-prime positive integers and such that

√7 =  , b ≠ 0

So, a = √7 b

Squaring both sides, we have

a² = 7b² …… (i)

⇒ 7 divides a² ⇒ 7 divides a

So, we can write

a = 7c (where c is an integer)

Putting the value of a = 7c in (i), we have

49c² = 7b² 7² = b²

It means 7 divides b² and so 7 divides b.

So, 7 is a common factor of both a and b which is a contradiction.

So, our assumption that √7 is rational is wrong.

Hence, we conclude that √7 is an irrational number.

• Let us assume that 5 – √3 is rational.

So, 5 – √3 may be written as

5 – √3 = , where p and q are integers, having no common factor except 1 and q ≠ 0.

⇒ 5 –  = √3 ⇒ √3 =

Since  is a rational number as p and q are integers.

∴ √3 is also a rational number which is a contradiction.

Thus, our assumption is wrong.

Hence, 5 – √3 is an irrational number.

• Since 2160 > 847 we apply the division lemma to 2160 and 847

we have, 2160 847 × 2 + 466

Since remainder 466 ≠ 0. So, we apply the division lemma to 847 and 466

847 = 466 × 1+ 381

Again remainder 381 ≠ 0. So we again apply the division lemma to 466 and 381.

466 = 381 × 1 + 85

Again remainder 85 ≠0. So, we again apply the division lemma to 381 and 85

381 = 85 × 4 + 41

Again remainder 41 ≠ 0. So, we again apply the division lemma to 85 and 41.

85 = 41 × 2 + 3

Again remainder 3 ≠ 0. So, we again apply the division lemma to 4 1 and 3.

41 = 3 × 13 + 2

Again remainder 2 ≠ 0. So, we again apply the division lemma to 3 and 2.

3 = 2 × 1 + 1

Again remainder 1 ≠ 0. So, we apply division lemma to 2 and 1

2 = 1 × 2 + 0

The remainder now becomes O. So, our procedure stops.

Since the divisor at this stage is 1.

Hence, HCF of 847 and 2160 is 1 and numbers are co-prime.

• If the number 6ⁿ, for any n, were to end with the digit zero, then h would bc divisible by 5. That is, the prime factorisation of 6ⁿ would contain the prime 5. But 6ⁿ = (2 × 3)ⁿ = 2ⁿ × 3n So the primes in factorisation of 6n are 2 and 3. So the uniqueness of the Fundamental Theorem of Arithmetic guarantees that (here are no other primes except 2 and 3 in the factorisation of 6n. So there is no natural number n for which 6” ends with digit zero.
• Let there be a positive integer n for which  be rational number.

⇒ is also perfect. square of positive integer From (A) and (B)

and  are perfect squares of positive integer. It contradict the fact that two perfect squares differ at least by 3.

Hence, there is no positive integer n for which  +  is rational.

1. It is given that on dividing 398 by the required number, there is a remainder of 7. This means that 398 – 7 = 391 is exactly divisible by the required timber In other words, required number is a factor of 391.

Similarly, required positive integer is a Íctor of 436 – 11 = 425 and 542 – 15 = 527

Clearly, the required number is the HCF of 391, 425 and 527.

Using the factor tree, we get the prime factorisations of 391, 425 and 527 as follows:

391 = 17 × 23, 425 52 × 17 and 527 17 × 31

∴ HCF of 391, 425, and 527 is 17.

Hence, the required number = 17.

Case Study Answers:

1.       Answer :
2. (d) No value of n.

Solution:

For a number to end in zero it must be divisible by 5, but 4ⁿ = 2²ⁿ is never divisible by 5. So, 4ⁿ never ends in zero for any value of n.

1. (c) For all n > 1.

Solution:

We know that product of two rational numbers is also a rational number.

So, a² = a × a = rational number.

a³ = a² × a = rational number.

a⁴ = a³ × a = rational number.

………………………………..

………………………………..

aⁿ = a^n-1 × a = rational number.

1. (d) Both (a) and (b).

Solution:

Let x = 2m + 1 and y = 2k + 1

Then x² +y² = (2m + 1)² + (2k + 1)²

= 4m² + 4m + 1 + 4k² + 4k + 1

= 4(m² + k² + m + k) + 2

So, it is even but not divisible by 4.

1. (a) Always true.

Solution:

Let three consecutive positive integers be n, n + 1 and n + 2.

We know that when a number is divided by 3, the remainder obtained is either 0 or 1 or 2.

So, n = 3p or 3p + 1 or 3p + 2, where pis some integer.

If n = 3p, then 2 is divisible by 3.

If n = 3p + 1, then n + 2 = 3p + 1 + 2 = 3p + 3 = 3(p + 1) is divisible by 3.

If n = 3p + 2, then n + 1 = 3p + 2 + 1 = 3p + 3 = 3(p + 1) is divisible by 3.

So, we can say that one of the numbers among n, n + 1 and n + 2 is always divisible by 3.

• (d) 8

Solution:

Any odd number is of the form of (2k + 1), where k is any integer.

So, n² – 1 = (2k + 1)² – 1 = 4k² + 4k

For k = 1, 4k² + 4k = 8, which is divisible by 8.

Similarly, for k = 2, 4k² + 4k = 24, which is divisible by 8.

And fork= 3, 4k² + 4k = 48, which is also divisible by 8.

So, 4k² + 4k is divisible by 8 for all integers k, i.e., n² – 1 is divisible by 8 for all odd values of n.

• Answer :

1. (b) 12240cm

Solution:

Here 80 = 24 × 5, 85 = 17 × 5

and 90 = 2 × 32 × 5

L.C.M of 80, 85 and 90 = 24 × 3 × 3 × 5 × 17 = 12240

Hence, the minimum distance each should walk when they at first time is 12240cm.

1. (c) 27

Solution:

Here 594 = 2 × 33 × 11 and 189 = 33 × 7

HCF of 594 and 189 = 3³ = 27

Hence, the maximum number of columns in which they can march is 27.

1. (c) 12 litres

Solution:

Here 768 = 28 × 3 and 420 = 22 × 3 × 5 × 7

HCF of 768 and 420 = 22 × 3 = 12

So, the container which can measure fuel of either tanker exactly must be of 12 litres.

1. (b) 75cm

Solution:

Here, Length = 825cm, Breadth = 675cm and Height = 450cm

Also, 825 = 5 × 5 × 3 × 11, 675 = 5 × 5 × 3 × 3 × 3 and 450 = 2 × 3 × 3 × 5 × 5

HCF = 5 × 5 × 3 = 75

Therefore, the length of the longest rod which can measure the three dimensions of the room exactly is 75cm.

• (a) 3 and 2

Solution:

LCM of 8 and 12 is 24.

Assertion Reason Answer-

2.Polynomials

1. What is a polynomial?

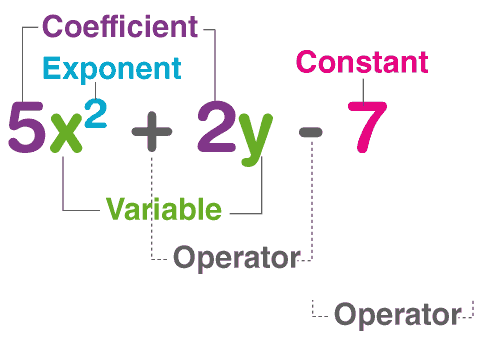
A polynomial p(x) in one variable x is an algebraic expression in x of the form P(x) = a_nxⁿ + a_n-1x^{n -1} + a_n-2x^n-2 + ………….. + a₂x² + a₁x + a₀, where x is a variable

1. a0, a1, a2 ……na are res pectively the coefficients of x0, x1, x2, x3, …… xn.
2. Each of a_nxⁿ, a_n-1 x^n-1, a_n-2x^n-2, ……… a₂x², a₁x, a₀, with a_n ≠ 0, is called the term of a polynomial.
3. The highest exponent of the variable in a polynomial determines the degree of the polynomial.
4. Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x² + x – 12. In this example, there are three terms: x2, x and -12.

The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial can have any number of terms but not infinite. Learn about degree, terms, types, properties, polynomial functions in this article.

1. Types of polynomials
2. A polynomial of degree zero is called a constant polynomial. Examples:
3. A polynomial of degree one is called a linear polynomial. It is of the form ax + b.

Examples: x – 2, 4y + 89, 3x – z.

1. A polynomial of degree two is called a quadratic polynomial. It is of the form ax² + bx + c, where a, b, c are real numbers and a ≠ 0.

Examples: x² – 2x + 5, x² – 3x etc.

1. A polynomial of degree 3 is called a cubic polynomial and has the general form ax³ + bx² + cx +d.

For example: x3 + 2×2- 2x + 5 etc.

Monomial: A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:

• 5x
• 3
• 6a⁴
• -3xy

Binomial: A binomial is a polynomial expression which contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:

• – 5x + 3,
• 6a⁴ + 17x
• xy² + xy

Trinomial

A trinomial is an expression which is composed of exactly three terms. A few examples of trinomial expressions are:

• – 8a⁴ + 2x + 7
• 4x² + 9x + 7
• Value of the polynomial

If p(x) is a polynomial in x, and k is a real number then the value obtained after replacing x by k in p(x) is called the value of p(x) at x = k which is denoted by p(k).

• Zero of a polynomial
• A real number k is said to be the zero of the polynomial p(x), if p(k) = 0.
• Zeroes of the polynomial can be obtained by solving the equation p(x) = 0.
• It is possible that a polynomial may not have a real zero at all.
• For any linear polynomial ax + b, the zero is given by the expression (-b/a) = -(constant term)/(Coefficient of x).
• Number of zeroes of a polynomial
• The number of real zeros of the polynomial is the number of times its graph touches or intersects x- axis.
• The graph of a polynomial p(x) of degree n intersects or touches the x-axis at at most n points.
• A polynomial of degree n has at most n distinct real zeroes.
• A linear polynomial has at most one real zero.

Linear Polynomial having no zero.
Linear Polynomial having one zero.

• A quadratic polynomial has at most two real zeroes.

Quadratic Polynomial having no zeroes.
Quadratic Polynomial having one zero.
Quadratic Polynomial having two zeroes.

• A cubic polynomial has at most three real zeroes.

Cubic Polynomial having no zeroes.
Cubic Polynomial having one zero.
Cubic Polynomial having one zeroes.
Cubic Polynomial having three zeroes.

• Relationship between zeroes and coefficients of a polynomial:
• For a linear polynomial ax + b, a ≠ 0, the zero is  It can be observed that:

1. For a quadratic polynomial ax² + bx + c, a ≠ 0,

Sum of the zeroes 

Product of the zeroes

1. For a cubic polynomial ax³ + bx² + cx + d = 0, a ≠ 0,

Sum of zeroes

Sum of the product of zeroes taken two at a time

Product of zeroes

• The quadratic polynomial whose sum of the zeroes  and product of zeroes  is given by: k [x² – x + ], where k is real.

If a, b and g are the zeroes of a cubic polynomial f (x)= ax³ + bx² + cx + d, a¹ 0, then

f(x) = k (x – a)(x – b) (x – g)

f (x)= k {x³ – (a + b + g )x² + (ab + bg + ga )x – abg}, where k is any non-zero real number.

1. Process of dividing a polynomial f(x) by another polynomial g(x) is as follows:

Step 1: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor. Then carry out the division process.

Step 2: To obtain the second term of the quotient, divide the highest degree term of the new dividend by the highest degree term of the divisor. Then again carry out the division process

Step 3: Continue the process till the degree of the new dividend is less that the degree of the divisor. This will be called the remainder.

1. Division Algorithm for polynomials: If f(x) and g(x) are any two polynomials, where g(x) ≠ 0, then there exists the polynomials q(x) and r(x) such that f(x) = g(x) q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x)

So, q(x) is the quotient and r(x) is the remainder obtained when the polynomial f(x) is divided by the polynomial g(x).

1. Factor of the polynomial

If f(x) = g(x) q(x) + r(x) and r(x) = 0, then polynomial g(x) is a factor of the polynomial f(x).

1. Finding zeroes of a polynomial using division algorithm

Division algorithm can also be used to find the zeroes of a polynomial. For example, if ‘a’ and ‘b’ are two zeroes of a fourth degree polynomial f(x), then other two zeroes can be found out by dividing f(x) by (x-a)(x-b).

1. Properties

Some of the important properties of polynomials along with some important polynomial theorems are as follows:

Property 1: Division Algorithm

If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then,

P(x) = G(x) • Q(x) + R(x)

Property 2: Bezout’s Theorem

Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.

Property 3: Remainder Theorem

If P(x) is divided by (x – a) with remainder r, then P(a) = r.

Property 4: Factor Theorem

A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).

Property 5: Intermediate Value Theorem

If P(x) is a polynomial, and P(x) ≠ P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x, y].

Property 6

The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,

Degree (P ± Q) ≤ Degree (P or Q)

Degree (P × Q) = Degree (P) + Degree(Q)

Property 7

If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.

Property 8

If a polynomial P is divisible by two coprime polynomials Q and R, then it is divisible by (Q • R).

Important Questions

Multiple Choice questions-

1. If one zero of the quadratic polynomial x² + 3x + k is 2, then the value of k is

(a) 10

(b) -10

(c) 5

(d) -5

2. If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then

(a) a = -7, b = -1

(b) a = 5, b = -1

(c) a = 2, b = -6

(d) a – 0, b = -6

3. The number of polynomials having zeroes as -2 and 5 is

(a) 1

(b) 2

(c) 3

(d) more than 3

4. If one of the zeroes of the cubic polynomial x3 + ax² + bx + c is -1, then the product of the other two zeroes is

(a) b – a + 1

(b) b – a – 1

(c) a – b + 1

(d) a – b – 1

5. The zeroes of the quadratic polynomial x² + 99x + 127 are

(a) both positive

(b) both negative

(c) one positive and one negative

(d) both equal

5. The zeroes of the quadratic polynomial x² + kx + k, k? 0,

(a) cannot both be positive

(b) cannot both be negative

(c) are always unequal

(d) are always equal

6. If the zeroes of the quadratic polynomial ax² + bx + c, c # 0 are equal, then

(a) c and a have opposite signs

(b) c and b have opposite signs

(c) c and a have the same sign

(d) c and b have the same sign

7. If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it

(a) has no linear term and the constant term is negative.

(b) has no linear term and the constant term is positive.

(c) can have a linear term but the constant term is negative.

(d) can have a linear term but the constant term is positive.

8. The number of polynomials having zeroes as 4 and 7 is

(a) 2

(b) 3

(c) 4

(d) more than 4

9. A quadratic polynomial, whose zeores are -4 and -5, is

(a) x²-9x + 20

(b) x² + 9x + 20

(c) x²-9x- 20

(d) x² + 9x- 20

10. The zeroes of the quadratic polynomial x² + 1750x + 175000 are

(a) both negative

(b) one positive and one negative

(c) both positive

(d) both equal

       Very Short Questions:

1. What will the quotient and remainder be on division of ax² + bx + c by px² + qx² + rx + 5, p ≠ 0?
2. If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?
3. Can x – 2 be the remainder on division of a polynomial p(x) by x + 3?
4. Find the quadratic polynomial whose zeros are -3 and 4.
5. If one zero of the quadratic polynomial x² – 5x – 6 is 6 then find the other zero.
6. If both the zeros of the quadratic polynomial ax² + bx + c are equal and opposite in sign, then find the value of b.
7. What number should be added to the polynomial x² – 5x + 4, so that 3 is the zero of the polynomial?
8. Can a quadratic polynomial x² + kx + k have equal zeros for some odd integer k > 1?
9. If the zeros of a quadratic polynomial ax² + bx + c are both negative, then can we say a, b and c all have the same sign? Justify your answer.
10. If the graph of a polynomial intersects the x-axis at only one point, can it be a quadratic polynomial?
11. If the graph of a polynomial intersects the x-axis at exactly two points, is it necessarily a quadratic polynomial?

Short Questions :

1. If one of the zeros of the quadratic polynomial f(x) = 4x² – 8kx – 9 is equal in magnitude but opposite in sign of the other, find the value of k.
2. If one of the zeros of the quadratic polynomial (k – 1)x² + kx + 1 is -3 then find the value of k.
3. If 1 is a zero of the polynomial p(x) = ax² – 3(a – 1)x -1, then find the value of a.
4. If α and β are zeros of polynomial p(x) = x² – 5x + 6, then find the value of α + B – 3aß.
5. Find the zeros of the polynomial p(x) = 4x² – 12x + 9.
6. What must be subtracted from p(x) = 8x⁴ + 14x³ – 2x² + 7x – 8 so that the resulting polynomial is exactly divisible by g(x) = 4x² + 3x – 2?
7. What must be added to f(x) = 4x⁴ + 2x³ – 2x² + x – 1 so that the resulting polynomial is divisible by g(x) = x² + 2x – 3?
8. Obtain the zeros of quadratic polynomial 3x² – 8x + 4√3 and verify the relation between its zeros and coefficients.
9. If α and β are the zeros of the polynomial 6y2 – 7y + 2, find a quadratic polynomial whose zeros are  and .
10. If one zero of the polynomial 3x² – 8x + 2k + 1 is seven times the other, find the value of k.

Long Questions :

1. Verify that the numbers given alongside the cubic polynomial below are their zeros. Also verify the relationship between the zeros and the coefficients.

x³ – 4x² + 5x – 2; 2,1,1

• Find a cubic polynomial with the sum of the zeros, sum of the products of its zeros taken two at a time, and the product of its zeros as 2, -7, -14 respectively.
• Find the zeros of the polynomial f(x) = x3 – 5x² – 2x + 24, if it is given that the product of its two zeros is 12.
• If the remainder on division of x³ – kx² + 13x – 21 by 2x – 1 is -21, find the quotient and the value of k. Hence, find the zeros of the cubic polynomial x³ – kx² + 13x.
• Obtain all other zeros of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeros are  and  .
• Given that √2 is a zero of the cubic polynomial 6x³ + √2x² – 10x – 4√2, find its other zeros.
• If α, β, γ bezerosofpo1ynomial 6x³ + 3x² – 5x + 1, then find die value of α-1 + β-1 + γ-1.
• Find the zeros of the polynomial f(x) = – 12x² + 39x – 28, if it is given that the zeros are in AP.

Case Study Questions:

1. ABC construction company got the contract of making speed humps on roads. Speed humps are parabolic in shape and prevents overspeeding, minimise accidents and gives a chance for pedestrians to cross the road. The mathematical representation of a speed hump is shown in the given graph.

Based on the above information, answer the following questions.

1. The polynomial represented by the graph can be ____ polynomial.
2. Linear
3. Quadratic
4. Cubic
5. Zero
6. The zeroes of the polynomial represented by the graph are:
7. 1, 5
8. 1, -5
9. -1, 5
10. -1, -5
11. Sum of zeroes of the polynomial represented by the graph are:
12. 4
13. 5
14. 6
15. 7
16. If  and β are the zeroes of the polynomial represented by the graph such that β > , β > , then |8  + β| = |8  + β| =
17. 1
18. 2
19. 3
20. 4
21. The expression of the polynomial represented by the graph is:
22. x² – 4x – 5
23. x² + 4x + 5
24. x² + 4x – 5
25. -x² + 4x + 5
26. While playing in garden, Sahiba saw a honeycomb and asked her mother what is that. She replied that it’s a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is parabolic. The mathematical representation of the honeycomb structure is shown in the graph .

Based on the above information, answer the following questions.

1. Graph of a quadratic polynomial is _____ in shape.
2. Straight line.
3. Parabolic.
4. Circular.
5. None of these.
6. The expression of the polynomial represented by the graph is:
7. x² – 49
8. x² – 64
9. x² – 36
10. x² – 81
11. Find the value of the polynomial represented by the graph when x = 6.
12. -2
13. -1
14. 2
15. 1
16. The sum of zeroes of the polynomial x² + 2x – 3 is:
17. -1
18. -2
19. 2
20. 1
21. If the sum of zeroes of polynomial at² + 5t + 3a is equal to their product, then find the value of a.
22. -5
23. -3
24. 5353
25. −53−53

Assertion reason questions-

1. Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
2. Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
3. Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
4. Assertion (A) is true but reason (R) is false.
5. Assertion (A) is false but reason (R) is true.

Assertion: x² + 7x + 12 has no real zeroes.

Reason: A quadratic polynomial can have at the most two zeroes.

• Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
• Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
• Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
• Assertion (A) is true but reason (R) is false.
• Assertion (A) is false but reason (R) is true.

Assertion: If the sum of the zeroes of the quadratic polynomial x²-2kx+8 is 2 then value of k is 1.
Reason: Sum of zeroes of a quadratic polynomial ax²+bx+c is -b/a

Answer Key-

Multiple Choice questions-

1. (b) -10
2. (d) a – 0, b = -6
3. (d) more than 3
4. (a) b – a + 1
5. (b) both negative
6. (a) cannot both be positive
7. (c) c and a have the same sign
8. (a) has no linear term and the constant term is negative.
9. (d) more than 4
10. (b) x² + 9x + 20
11. (a) both negative

Very Short Answer :

1. 0, ax² + bx + C.
2. Since the quotient is zero, therefore

deg p(x) < deg g(x)

• No, as degree (x – 2) = degree (x + 3)
• Sum of zeros = -3 + 4 = 1,

Product of zeros = – 3 x 4 = -12

∴ Required polynomial = x² – x – 12

• Let α,6 be the zeros of given polynomial.

Then α + 6 = 5 3 ⇒ α = -1

• Let α and -α be the roots of given polynomial.

Then α + (-α) = 0 ⇒  = 0 ⇒ b = 0.

• Let f(x) = x² – 5x + 4

Then f(3) = 3² – 5 x 3 + 4 = -2

For f(3) = 0, 2 must be added to f(x).

• No, for equal zeros, k = 0, 4 ⇒ k should be even.
• Yes, because  = sum of zeros < 0, so that  = 0 > 0. Also the product of the zeros = = 0 > 0.
• Yes, because every quadratic polynomial has at the most two zeros.
• No, x⁴ – 1 is a polynomial intersecting the x-axis at exactly two points.

Short Answer :

1. Let one root of the given polynomial be α.

Then the other root = -α

Sum of the roots = (-α) + α = 0

• Since – 3 is a zero of the given polynomial

∴ (k – 1)(-3)² + k(-3) + 1 = 0 :

⇒ 9k – 9 – 3k + 1 = 0 ⇒ k = 4/3.

• Put x = 1 in p(x)

∴ p(1) = a(1)² – 3(a – 1) x 1 – 1 = 0

⇒ a – 3a + 3 – 1 = 0 ⇒ 2a = -2 ⇒ a = 1

• Here, α + β = 5, αβ = 6

= α + β – 3αβ = 5 – 3 x 6 = -13

• p(x) = 4x² – 12x + 9 = (2x – 3)+

For zeros, p(x) = 0

⇒ (2x – 3)(2x – 3) = 0 ⇒ x =

• Let y be subtracted from polynomial p(x)

: 8x⁴ + 14x³ – 2x² + 7x – 8 – y is exactly divisible by g(x)

Now,

∵ Remainder should be 0.

∴ 14x – 10 – y = 0 or 14x – 10 = y or y = 14x – 10

∴ (14x – 10) should be subtracted from p(x) so that it will be exactly divisible by g(x)

• By division algorithm, we have

f(x) = g(x) × q(x) + r(x)

= f(x) – r(x) = g(x) × q(x) ⇒ f(x) + {-r(x)} = g(x) × q(x)

Clearly, RHS is divisible by g(x). Therefore, LHS is also divisible by g(x). Thus, if we add –r(x) to f(x), then the resulting polynomial is divisible by g(x). Let us now find the remainder when f(x) is divided by g(x).

∴ r(x) = -61x + 65 or -r(x) = 61x – 65

Hence, we should add –r(x) = 61x – 65 to f(x) so that the resulting polynomial is divisible by g(x).

• We have,

• Let p(y) = 6y² – 7y + 2

1. Let α and β be the zeros of the polynomial. Then as per question β = 7α

Long Answer :

1. Let p(x) = x³ – 4x² + 5x – 2

On comparing with general polynomial px) ax³ + bx² + cx + d, we get a = 1, b = -4, c = 5 and d = -2

Given zeros 2, 1, 1.

∴ p(2) = (2)³ – 4(2)² + 5(2) – 2 = 8 – 16 + 10 – 2 = 0

and p(1) = (1)³ – 4(1)² + 5(1) – 2 = 1 – 4 + 5 – 2 = 0

Hence, 2, 1 and I are the zeros of the given cubic polynomial.

Again, consider α = 2, β = 1, γ = 1

∴ α + 13 + y = 2 + 1 + 1 = 4

• Let the cubic polynomial be p(x) = ax³ + bx² + cx + d. Then

p(x) = a[x³ + (-2)x² + (-7)x + 14] ⇒ p(x) = a[x³ – 2x² – 7x + 14]

For real value of a = 1, p(x) = x³ – 2x² – 7x + 14

• Let α, β and γ be the zeros of polynomial (fx) such that αβ = 12.

Now, α + β + γ = 5 α + β – 2 = 5

= α + β = 7 a = 7 – β

= (7 – β) β =12 ⇒ 7β – β² – 12

= β² + 7β + 12 = 0 ⇒ β² – 3β – 4β + 12 = O

= β = 4 or β = 3

β = 4 or β = 3

∴ α = 3 or α = 4

• Let f(x) = x³ – kx² + 13x – 21

•  

• The given polynomial is f(x) = (6x³ +√2x² – 10x – 4√2). Since √2 is the zero of f(x), it follows that (x – √2) is a factor of f(x).

On dividing f(x) by (x – √2), we get

• ∵ p(x) = 6×3 + 3×2 – 5x + 1 so a = 6, b = 3, c = -5, d = 1

∴ α, β and γ are zeros of the polynomial p(x).

• If α, β, γ are in AP., then,

β – α = γ + β ⇒ 2β = α + γ

α + β + γ =  =  = 12 ⇒ α + γ = 12 – β …….. (i)

From (i) and (ii)

2β = 12 – β or 3β = 12 or β = 4

Putting the value of β in (i), we have

8 = a + γ

αβγ =  …….. (iii)

(αγ) 4 = 28 or αγ = 7 or γ = 7α ….. (iv)

Putting the value of γ = 7α in (iii), we get

⇒ 8 = α +  ⇒ 8α = α² + 7

⇒ α² – 8α + 7 = 0 ⇒ α² – 7α – 1α + 7 = 0

⇒ α(α – 7)-1 (α – 7) = 0 ⇒ (α – 1)(α – 7) = 0

⇒ α = 1 or α = 7

Case Study Answers:

1. Answer :
2. (b) Quadratic

Solution:

Since, the given graph is parabolic is shape, therefore it will represent a quadratic polynomial.

[∵ Graph of quadratic polynomial is parabolic in shape)

1. (c) -1, 5

Solution:

Since, the graph cuts the x-axis at -1, 5. So the polynomial has 2 zeroes i.e., -1 and 5.

1. (a) 4

Solution:

Sum of zeroes = -1 + 5 = 4

1. (c) 3

Solution:

Since α and β are zeroes of the given polynomial and β > α, β > α,

∴ α = -1 ∴ α = -1 and β = 5β = 5

∴ |8α + β| = |8(-1) + 5| = | -8 + 5| = |-3| = 3.

∴|8α + β|=|8(−1)+5|=|−8+5|=|−3|=3.

• (d) -x² + 4x + 5

Solution:

Since the zeroes of the given polynomial are -1 and 5.

∴ Required polynomial p(x)

= k² {x² – (-1 + 5)x + (-1)(5)} = k(x² – 4x – 5)

For k = -1, we get,

p(x) = -x² + 4x + 5, which is the required polynomial.

• Answer :
• (b) Parabolic.

Solution:

Graph of a quadratic polynomial is a parabolic in shape.

1. (c) x² – 36

Solution:

Since the graph of the polynomial cuts the x-axis at (-6, 0) and ( 6, 0). So, the zeroes of polynomial are -6 and 6.

∴ Required polynomial is

p(x) = x² – (-6 + 6)x + (-6)(6) = x² – 36

1. (c) 2

Solution:

We have, p(x) = x² – 36

Now, p(6) = 6² – 36 = 36 – 36 = 0

1. (b) -2

Solution:

Let f(x) = x² + 2x – 3. Then,

• (d) −53−53

Solution:

The given polynomial is at² + 5t + 3a

Given, sum of zeroes = product of zeroes

Assertion Reason Answer-

1. (d) Assertion (A) is false but reason (R) is true.
2. (a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).